Rappel sur la notion d'orbitale

L'expérience — l'effet photoélectrique, la spectroscopie, etc. — montre que l'énergie des atomes pris individuellement, en particulier celle de leurs électrons, est quantifiée et que les atomes doivent être abordés par la physique quantique. Il en va de même pour les ensembles d'atomes : molécules, édifices cristallins, etc. Les propriétés courantes de la matière, en dehors des réactions nucléaires, résultant uniquement d'interactions électrostatiques, il est indispensable de disposer d'une bonne description des cortèges électroniques des ensembles d'atomes pour en comprendre les propriétés. La localisation et l'énergie des électrons se décrivent à l'aide des orbitales. Si on examine en mécanique quantique le cas le plus simple qui existe, celui de l'atome d'hydrogène, on arrive en effet à une solution (qui passe par la résolution de l'équation de Schrödinger) qui se présente de manière très différente des solutions de la mécanique newtonienne pour deux particules :

• l'énergie du système noyau-électron ne peut pas prendre n'importe quelle valeur, mais est quantifiée ;
• toutes les propriétés de l'électron peuvent se déduire d'une fonction dite « fonction d'onde » $\psi$ qui est différente pour chaque valeur possible de l'énergie et qui est paramétrée par quatre nombres quantiques ; en particulier, la probabilité $\mathbb{P}_V$ de présence de l'électron dans un volume $V$ est donnée par la relation : $$\mathbb{P}_V = \iiint_V \psi \,\psi^* \,\mathrm{d}x \mathrm{d}y \mathrm{d}z $$ où $\psi^*$ est la fonction complexe conjuguée de $\psi$.

La notion de fonction d'onde apparaît dans le traitement quantique de n'importe quel système physique. S'agissant des atomes ou des molécules, on l'appelle souvent « orbitale ». En traçant la surface qui délimite un volume $v$ tel que $\mathbb{P}_v = 0{,}9$ (ou une autre valeur : par exemple $0{,}95$) on a accès à la forme de l'orbitale, c'est-à-dire de la zone de l'espace où la probabilité de présence l'électron est égale à $0{,}9$ (ou $0{,}95$). Finalement, le mot « orbitale » est souvent employé pour désigner cette zone de l'espace, mais en principe, il désigne la fonction d'onde. Bien évidemment :

$$ \iiint_{\text{tout l'espace}} \psi \,\psi^* \,\mathrm{d}x \mathrm{d}y \mathrm{d}z = 1 $$

Les orbitales atomiques des systèmes dit « hydrogénoïdes », c'est-à-dire à deux particules : un noyau et un électron, comme $\ce{H}$, $\ce{He+}$ ou $\ce{Li^2+}$ sont parfaitement connues à travers la résolution exacte des équations qui leurs sont associées. De bonnes approximation existent pour les orbitales atomiques des autres atomes et elles permettent de donner la configuration électronique d'un atome dans son état fondamental, par exemple $1s^2 \, 2s^2 \, 2p^3$ pour l'atome d'azote, $1s, 2s \text{ et } 2p$ renvoyant à des orbitales connues.

Orbitales de la molécule de dihydrogène

En présence de plus d'un noyau, l'étude des orbitales devient beaucoup plus compliquée : des nouvelles approximations doivent de nouveau être envisagées. L'une des plus simples est dite « combinaison linéaire d'orbitales atomiques » notée CLOA, dont le principe repose sur deux hypothèses :

• les électrons de cœur restent principalement sous l'influence du noyau de leur atome d'origine ;
• les orbitales de électrons de valence sont des combinaisons linéaires des orbitales des électrons de valence des atomes de la molécule.

L'application convenable de la méthode CLOA requiert la manipulation de l'équation de Schrödinger dans ce cadre simplifié et dépasse déjà l'objet de ce cours. Il est cependant possible d'en appréhender le principe en s'intéressant d'abord aux conditions de normalisation. Soit alors deux atomes d'hydrogène et les orbitales qui correspondent à leur état fondamental d'énergie $E_{\ce{H}}$ : $\psi_1$ l'orbitale 1s d'un des atomes et $\psi_2$ l'orbitale 1s de l'autre. L'hypothèse CLAO est que les orbitales moléculaires $\phi$ du dihydrogène prennent la forme :

$$ \phi=c_1 \psi_1 + c_2 \psi_2 $$

$c_1$ et $c_2$ étant deux scalaires que nous allons nous employer ici à déterminer.

La probabilité de trouver l'électron de cette orbitale dans un volume étendu à tout l'espace est égale à un : c'est la condition de normalisation :

$$ \int \phi\,\phi^{*}\,\mathrm{d}V =c_1^2\int \psi_1\,\psi_1^{*}\mathrm{d}V + c_2^2\int \psi_2\,\psi_2^{*}\,\mathrm{d}V + c_1c_2 \left[ \int \psi_2\,\psi_1^{*}\,\mathrm{d}V + \int \psi_1\,\psi_2^{*}\,\mathrm{d}V\right] =1 $$

Comme $\psi_1$ et $\psi_2$ sont des orbitales (atomiques) :

$$ \int \psi_1 \,\psi_1^{*} \, \mathrm{d}V = \int \psi_2 \,\psi_2^{*} \, \mathrm{d}V = 1$$

Les deux atomes étant par ailleurs indiscernables :

$$c_1^2 = c_2^2 = c^2 $$

ce qui entraîne :

$$ c_1 c_2 = c^2 \text{ ou } c_1 c_2 = -c^2 $$

Soit aussi $S$ l'intégrale de recouvrement :

$$ S= \int \psi_2\,\psi_1^{*}\,\mathrm{d}V = \int \psi_2^{*}\,\psi_1\,\mathrm{d}V $$

Deux solutions sont envisageables ; le premier cas : $\displaystyle{c_1 c_2 = c^2}$ donne une première valeur de $c$ grâce à la normalisation :

$$ 2c^2(1+S) = 1 \Rightarrow c= \frac{1}{\sqrt{2(1+S)}} $$

La racine négative de l'équation est totalement symétrique de la solution positive et n'est pas examinée. Le deuxième cas $\displaystyle{c_1 c_2 = -c^2}$ donne une autre valeur de normalisation associée à cette solution :

$$ 2c^2(1-S) = 1 \Rightarrow c= \frac{1}{\sqrt{2(1-S)}} $$

Finalement, les deux orbitales moléculaires obtenues par combinaison de $\psi_1$ et $\psi_2$ sont :

$$ \phi_{\sigma} = \frac{\psi_1+\psi_2}{\sqrt{2(1+S)}} \qquad\text{ et }\qquad \phi_{\sigma^*} = \frac{\psi_1-\psi_2}{\sqrt{2(1-S)}} $$

Ces deux orbitales moléculaires, respectivement nommées $\sigma$ et $\sigma^*$, présentent des énergies $E_{\sigma}$ et $E_{\sigma^*}$ telles que :

$$ E_{\sigma} < E_{\ce{H}} < E_{\sigma^*}$$ $$ E_{\ce{H}} - E_{\sigma} < E_{\sigma^*} - E_{\ce{H}} $$

En raison de ce classement, les deux électrons du dihydrogène occupent, dans l'état fondamental, l'orbitale $\sigma$. L'ensemble est alors plus stable que les deux atomes d'hydrogène séparés. Un examen plus approfondi montre que :

• $\sigma$ conduit à une forte probabilité de présence électronique entre les deux noyaux ;
• l'énergie de $\sigma$, qui varie avec la distance internucléaire, passe par un minimum pour 74 pm.

$\sigma$ est dite liante et $\sigma^*$ antiliante.

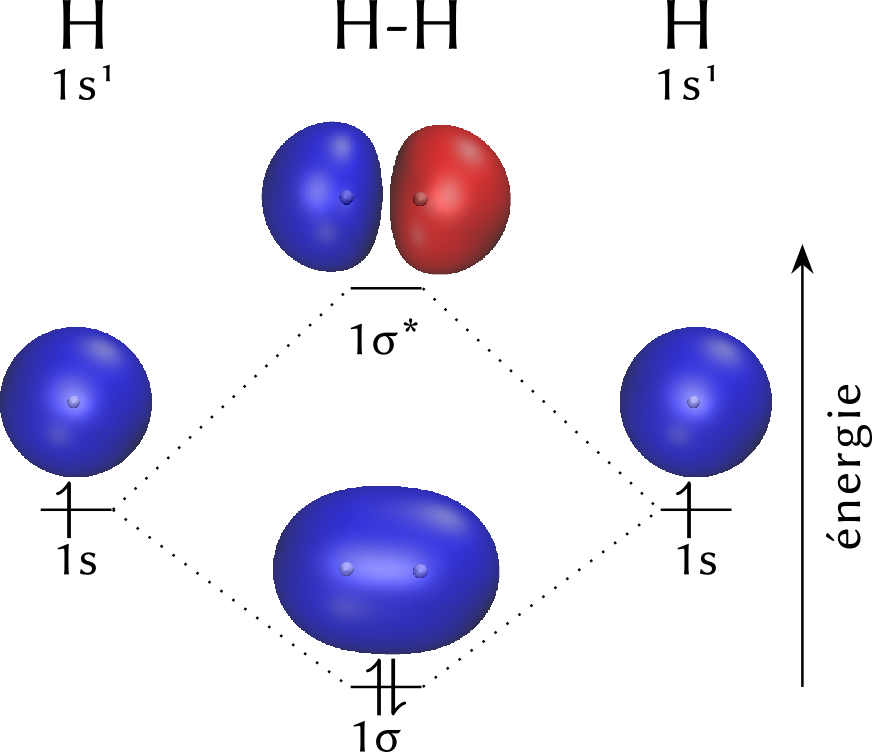
La connaissance du remplissage des orbitales moléculaires permet de retrouver plusieurs caractéristiques de la molécule :

• l'ordre (ou indice) de liaison : demi-différence entre le nombre d'électrons liants et le nombre d'électrons antiliants ; l'ordre de liaison recouvre la notion de liaison simple, double ou triple des représentations de Lewis ;
• le spin $S$ total de la molécule, qui se déduit du nombre d'électron non appariés ; ici S = 1/2 - 1/2 = 0$ puisque les deux électrons présents sont appariés et de spins opposés.

Ce type de résultat est généralisable aux combinaisons linéaires d'orbitales atomiques. Une orbitale dite liante est plus basse en énergie que les orbitales dont elle est issue par combinaison linéaire. Donc si un électron s'y trouve, on a un édifice plus stable que l'ensemble des atomes pris séparément. On constate que les orbitales liantes sont généralement (mais souvent pas uniquement) situées dans l'espace principalement entre les atomes de l'édifice. Des électrons situés entre des atomes et dont la présence stabilise le fait que ces atomes soient associés : voilà qui correspond bien à une idée de liaison.

Quand des électrons doivent se placer dans une orbitale antiliante (les liantes étant remplies, par exemple), l'édifice est déstabilisé car une orbitale antiliante a une énergie supérieure aux orbitales dont elle est issue par combinaison linéaire. Si un électron qui s'y trouve "déstabilise" l'édifice, il compte pour la suppression d'une demi-liaison.

En reprenant le schéma du dihydrogène pour envisager le dihélium, le remplissage conduit à deux électrons dans la $\sigma$ et deux dans la $\sigma^*$. L'indice de liaison égal à 1/2 + 1/2 - 1/2 -1/2 = 0. Comme $E_{\ce{He}} - E_{\sigma} < E_{\sigma^*} - E_{\ce{He}}$, le dihélium est moins stable que deux atomes d'hélium séparés et il n'existe pas.

De la même manière, une molécule de dihydrogène peut être cassée si un apport d'énergie : photon utltraviolet, chaleur (qui entraîne des vibrations moléculaires intense provoquent le passage d'un des deux électrons de $\sigma$ vers $\sigma^*$ et comme $E_{\ce{H}} - E_{\sigma} < E_{\sigma^*} - E_{\ce{H}}$ la molécule de $\ce{H2}$ ainsi formée est moins stable que deux atomes d'hydrogène séparés : elle se décompose.

Retour